D堆的C语言实现
D堆是二叉堆的简单推广,跟二叉堆的区别是所有的节点都有d个儿子,代码也跟二叉堆的相似。下图表示一个D=3的最小D堆。

D堆插入操作的时间改进为O(log(d,N)),然面删除操作要花费较大时间,一般需要O(d*log(d,N))。如果D不是2的幂,也不能通过二进制移位来实现乘法和除法,这样也大大增加运行时间。 大部分时候总是使用二叉堆,但D堆也在一些情况下使用。比如,插入操作多删除操作多很多时,或是优先队列太大不能完全装入内存时。
通常D堆也跟二叉堆一样以数组存储,层为 log(d,n),以下的代码来定义D堆结构。
typedef struct d_heap_s* d_heap_pt;
typedef struct d_heap_s {
int size;
int degree;
int current;
Item *data;
} d_heap_t;
当以数组存储时,D堆的父子节点下标存在如下关系。
- 索引为i的孩子的索引是 (i*d + j),其中j = 1, 2, ..., d;
- 索引为i的父结点的索引是 (i - 1) / d;
添加元素图解
D堆的元素插入步骤跟二叉树相同,在堆中添加元素时需要执行向上堆化操作,假设在最小堆中添加15,需要执行以下步骤。
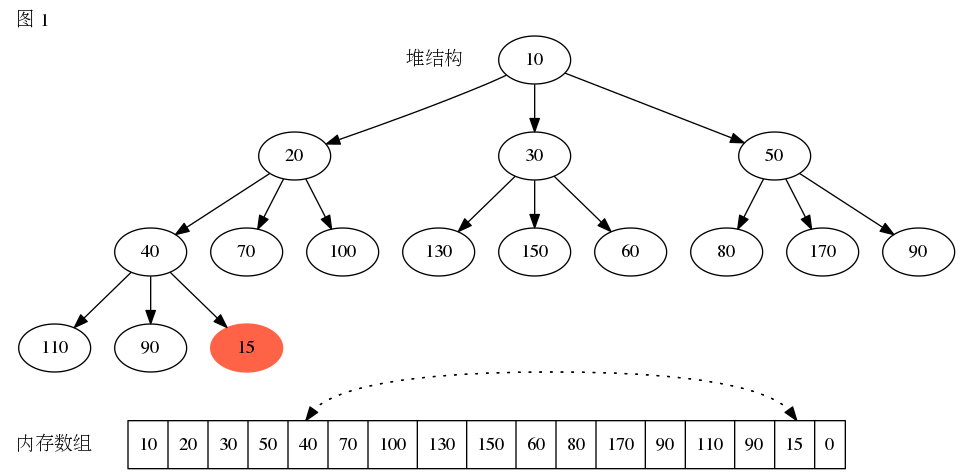
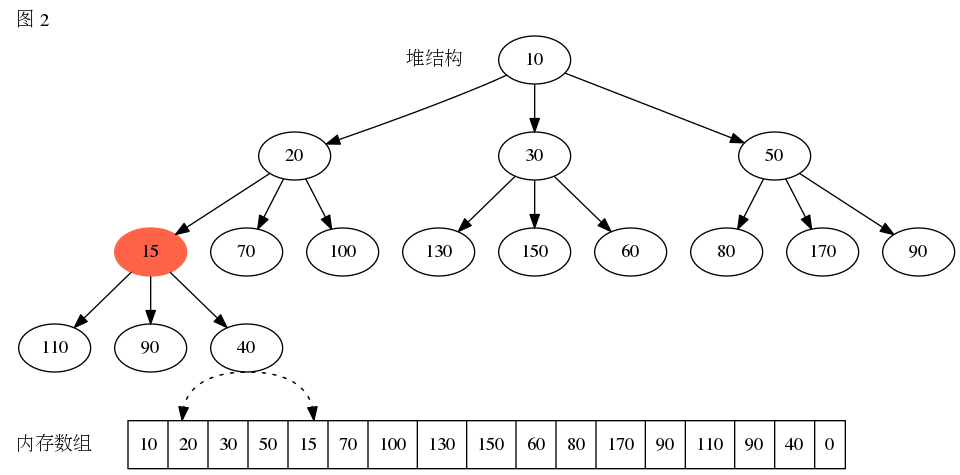
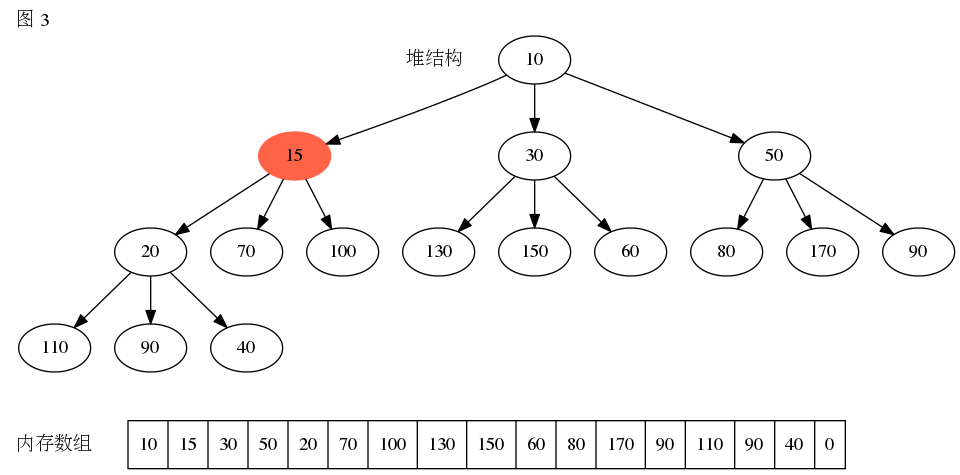
代码实现如下:
/*
* Name: fixup
* Description: 向上堆化
*
*/
static void
fixup(d_heap_pt heap, int k)
{
int degree = heap->degree;
while (k>0 && item_cmp(heap->data[(k - 1) / degree],heap->data[k])) {
swap(heap->data, k, (k - 1) / degree);
k = (k - 1) / degree;
}
}
int
d_heap_push(d_heap_pt heap, Item element)
{
if (heap == NULL) {
return 0;
}
if (heap->current == heap->size) {
return 0;
}
heap->data[heap->current] = element;
fixup(heap, heap->current++);
return 1;
}
删除堆顶元素图解
D堆的元素插入步骤也跟二叉树相同,在堆中移除堆顶元素时需要执行向下堆化操作,假设在最小堆中移除堆顶完素,需要执行以下步骤。
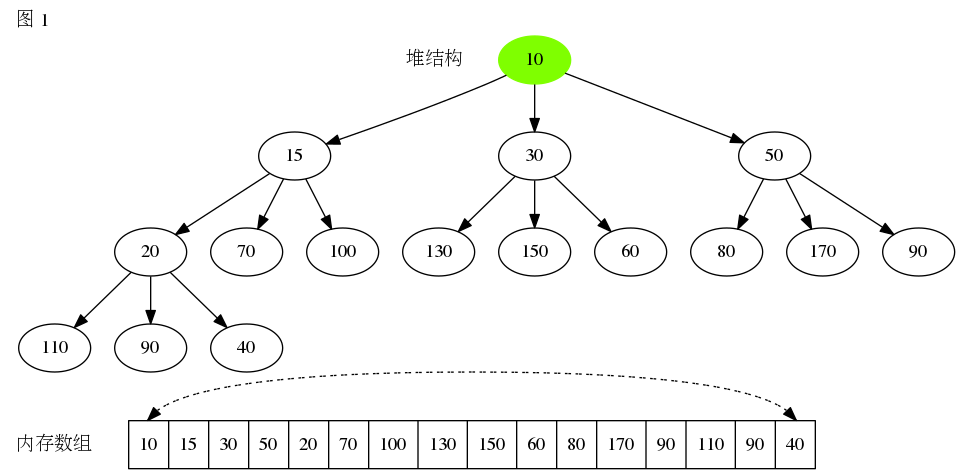
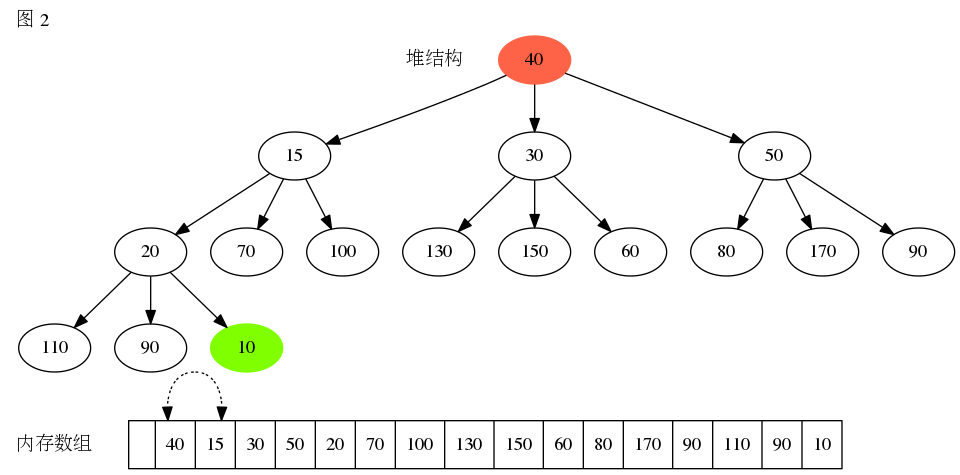
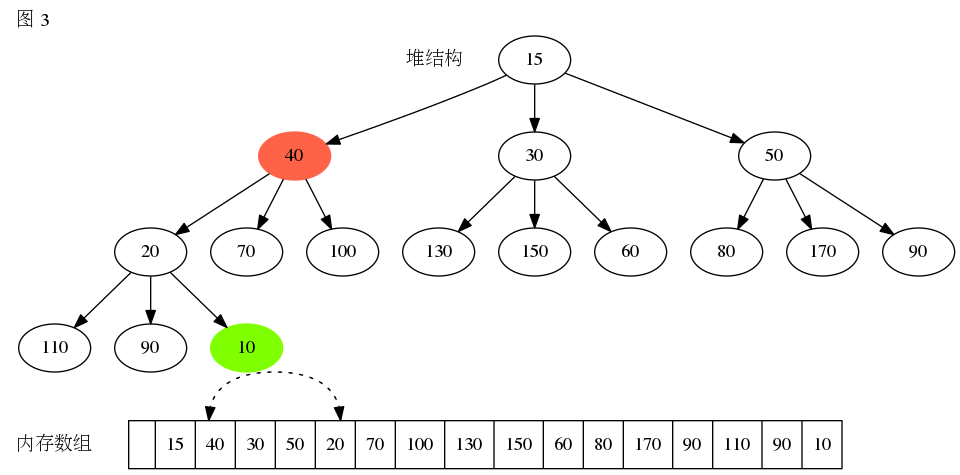
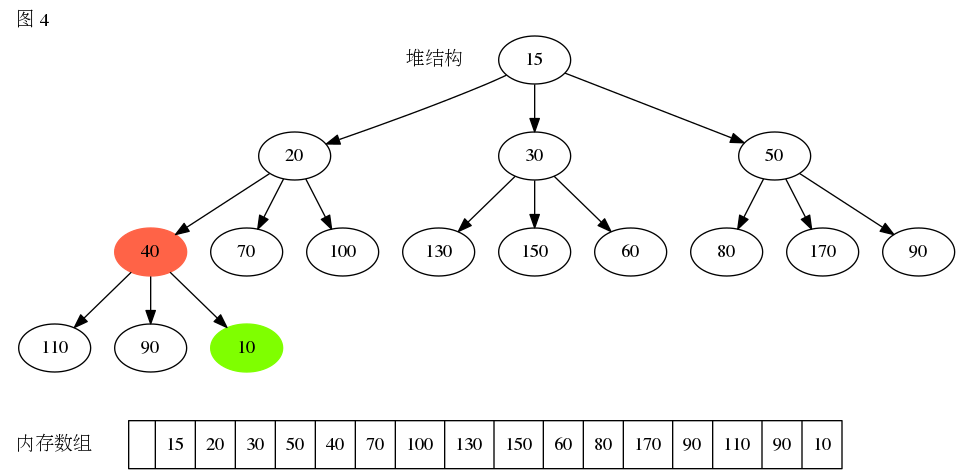
代码实现如下:
/*
* Name: fixdown
* Description: 向下堆化
*
*/
static void
fixdown(d_heap_pt heap, int k, int end)
{
int temp, tail, i;
int degree = heap->degree;
while (k*degree + 1 <= end) {
tail = k*degree + degree;
tail = tail < end ? tail : end;
for (i = k*degree + 1, temp = i; i < tail; i++) {
if (item_cmp(heap->data[temp], heap->data[i])) {
temp = i;
}
}
if (!item_cmp(heap->data[k], heap->data[temp])) {
break;
}
swap(heap->data, k, temp);
k = temp;
}
}
Item
d_heap_pop(d_heap_pt heap)
{
swap(heap->data, 0, heap->current - 1);
fixdown(heap, 0, heap->current - 2);
return heap->data[--heap->current];
}
完整源码
/* d_heap.h */
#ifndef D_HEAP_H
#define D_HEAP_H
typedef int Item;
typedef struct d_heap_s* d_heap_pt;
typedef struct d_heap_s {
int size;
int degree;
int current;
Item *data;
} d_heap_t;
d_heap_pt d_heap_init(int size, int degree);
void d_heap_free(d_heap_pt heap);
void d_heap_print(d_heap_pt heap);
int d_heap_push(d_heap_pt heap, Item element);
Item d_heap_pop(d_heap_pt heap);
Item d_heap_top(d_heap_pt heap);
int d_heap_empty(d_heap_pt heap);
#endif
d_heap.h
/* d_heap.c */
/*
* =====================================================================================
*
* Filename: d_heap.c
*
* Description: D堆实现
*
* Version: 1.0
* Created: 2016-09-23 22:00
* Revision: none
* Compiler: gcc
*
* Author: simon
*
* =====================================================================================
*/
#include <stdio.h>
#include <stdlib.h>
#include "d_heap.h"
static void
swap(Item *data, int a, int b)
{
Item c;
c = data[a];
data[a] = data[b];
data[b] = c;
}
/*
* 最小堆 ((a) > (b))
* 最大堆 ({a} < (b))
*
*/
#define item_cmp(a, b) ((a) > (b)) /* 最小堆 */
/*
* Name: fixup
* Description: 向上堆化
*
*/
static void
fixup(d_heap_pt heap, int k)
{
int degree = heap->degree;
while (k>0 && item_cmp(heap->data[(k - 1) / degree],heap->data[k])) {
swap(heap->data, k, (k - 1) / degree);
k = (k - 1) / degree;
}
}
/*
* Name: fixdown
* Description: 向下堆化
*
*/
static void
fixdown(d_heap_pt heap, int k, int end)
{
int temp, tail, i;
int degree = heap->degree;
while (k*degree + 1 <= end) {
tail = k*degree + degree;
tail = tail < end ? tail : end;
for (i = k*degree + 1, temp = i; i < tail; i++) {
if (item_cmp(heap->data[temp], heap->data[i])) {
temp = i;
}
}
if (!item_cmp(heap->data[k], heap->data[temp])) {
break;
}
swap(heap->data, k, temp);
k = temp;
}
}
d_heap_pt
d_heap_init(int size, int degree)
{
if (size<=0) {
return NULL;
}
d_heap_pt heap_pt = malloc(sizeof(d_heap_t));
heap_pt->data = malloc(sizeof(Item)*size);
heap_pt->size = size;
heap_pt->degree = degree;
heap_pt->current = 0;
return heap_pt;
}
void
d_heap_free(d_heap_pt heap)
{
if (heap == NULL) {
return;
}
free(heap->data);
free(heap);
}
void
d_heap_print(d_heap_pt heap)
{
int i;
if (heap == NULL) {
return;
}
for (i=0; i<heap->size; i++) {
printf("%d ", heap->data[i]);
}
}
int
d_heap_push(d_heap_pt heap, Item element)
{
if (heap == NULL) {
return 0;
}
if (heap->current == heap->size) {
return 0;
}
heap->data[heap->current] = element;
fixup(heap, heap->current++);
return 1;
}
Item
d_heap_pop(d_heap_pt heap)
{
swap(heap->data, 0, heap->current - 1);
fixdown(heap, 0, heap->current - 2);
return heap->data[--heap->current];
}
Item
d_heap_top(d_heap_pt heap)
{
return heap->data[0];
}
int
d_heap_empty(d_heap_pt heap)
{
return heap->current == 0;
}
d_heap.c
/* d_heap_test.c */
#include <stdlib.h>
#include <stdio.h>
#include "d_heap.h"
#define LENGTH(a) ( (sizeof(a)) / (sizeof(a[0])) )
int
main(int argc, char *argv[])
{
int a[] = {10, 20, 30, 50, 40, 70, 100, 130, 150, 60, 80, 170, 90, 110, 90};
int i, len=LENGTH(a);
d_heap_pt heap = NULL;
heap = d_heap_init(LENGTH(a) + 10, 3);
printf("\n== 空堆检查: %d", d_heap_empty(heap));
printf("\n== 插入数据: ");
for(i=0; i<len; i++)
{
printf("%d ", a[i]);
d_heap_push(heap, a[i]);
}
printf("\n== 空堆检查: %d", d_heap_empty(heap));
printf("\n== 最 小 堆: ");
d_heap_print(heap);
i=15;
d_heap_push(heap, i);
printf("\n== 添加元素: %d", i);
printf("\n== 最 小 堆: ");
d_heap_print(heap);
printf("\n== 堆顶元素: %d\n", d_heap_top(heap));
i = d_heap_pop(heap);
printf("\n== 删除元素: %d", i);
printf("\n== 最 小 堆: ");
d_heap_print(heap);
printf("\n");
i = d_heap_pop(heap);
printf("\n== 删除元素: %d", i);
printf("\n== 最 小 堆: ");
d_heap_print(heap);
printf("\n");
d_heap_free(heap);
return 0;
}
d_heap_test.c
测试程序的运行结果
== 空堆检查: 1
== 插入数据: 10 20 30 50 40 70 100 130 150 60 80 170 90 110 90
== 空堆检查: 0
== 最 小 堆: 10 20 30 50 40 70 100 130 150 60 80 170 90 110 90 0 0 0 0 0 0 0 0 0 0
== 添加元素: 15
== 最 小 堆: 10 15 30 50 20 70 100 130 150 60 80 170 90 110 90 40 0 0 0 0 0 0 0 0 0
== 堆顶元素: 10
== 删除元素: 10
== 最 小 堆: 15 20 30 50 40 70 100 130 150 60 80 170 90 110 90 10 0 0 0 0 0 0 0 0 0
== 删除元素: 15
== 最 小 堆: 20 40 30 50 90 70 100 130 150 60 80 170 90 110 15 10 0 0 0 0 0 0 0 0 0
转载文章请注明出处: http://mingnote.com