清风明月的笔记

AVL树的C语言实现

失去平衡的AVL树
AVL树的旋转
AVL树的插入
AVL树的删除
完整源码
测试程序的运行结果

AVL树是根据它的发明者G.M.Adelson-Velsky和E.M.Landis命名的。它是最先发明的自平衡二叉查找杩，也被称为高度平衡树。AVL树中任何节点的两个子树的高度最大差别为1。 AVL树的查找，插入，和删除在平均和最坏情况下都是O(log(n))。

AVL树的一般定义：

typedef struct avl_tree_s* avl_tree_pt;

typedef struct avl_tree_s {
    Item data;
    int height;
    avl_tree_pt left;
    avl_tree_pt right;
} avl_tree_t;

失去平衡的AVL树

如果在AVL树中插入或删除节点后，可能导致AVL树失衡，即树的左右高度差大于1。这时就需要对其进行旋转处理。

这种失去平衡的树可能有4种姿态：LL(左左),LR(左右),RR(右右),RL(右左)

LL(左左): 插入或删除一个节点后，左子树的高度比右子树的高度大2，且左子树的左子树的高度比左子树的右子树的高度大。如图所示

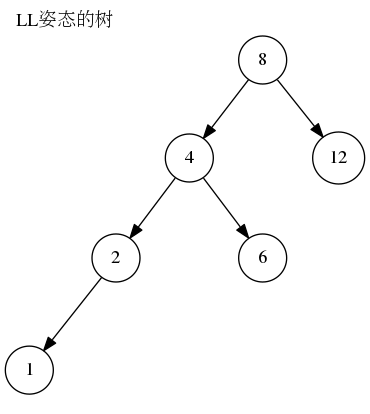
RR(右右): 插入或删除一个节点后，右子树的高度比左子树的高度大2，且右子树的右子树的高度比右子树的左子树的高度大。如图所示

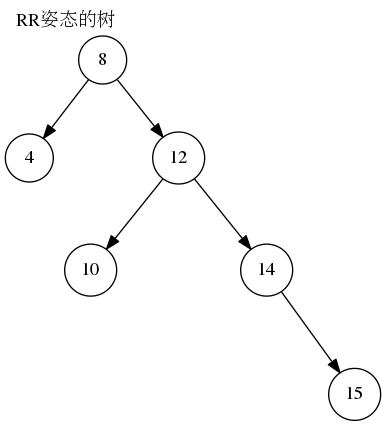
LR(左右): 插入或删除一个节点后，左子树的高度比右子树的高度大2，且左子树的左子树的高度比左子树的右子树的高度小。如图所示

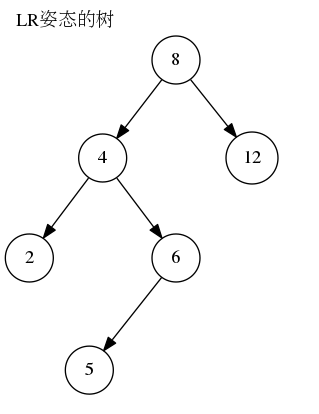
RL(右左): 插入或删除一个节点后，右子树的高度比左子树的高度大2，且右子树的右子树的高度比右子树的左子树的高度小。如图所示

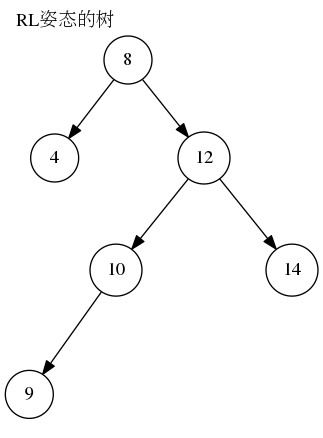
AVL树的旋转

LL失去平衡的情况，可以通过一次旋转恢复AVL树的平衡。如图所示

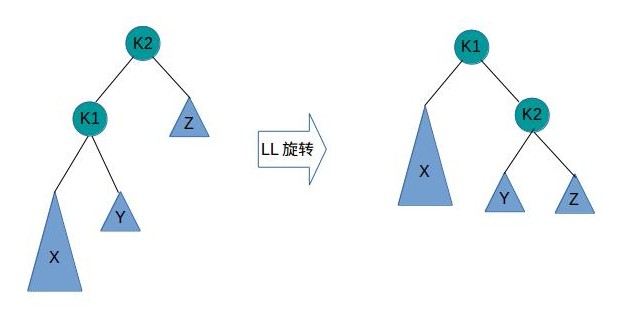
代码如下

static avl_tree_pt 
left_left_rotation(avl_tree_pt tree)
{
    avl_tree_pt left_child;

    left_child = tree->left;
    tree->left = left_child->right;
    left_child->right = tree;
    tree->height = MAX(HEIGHT(tree->left), HEIGHT(tree->right)) + 1;
    left_child->height = MAX(HEIGHT(left_child->left), HEIGHT(left_child->right)) + 1;

    return left_child;
}

RR失去平衡的情况，可以通过一次旋转恢复AVL树的平衡。如图所示

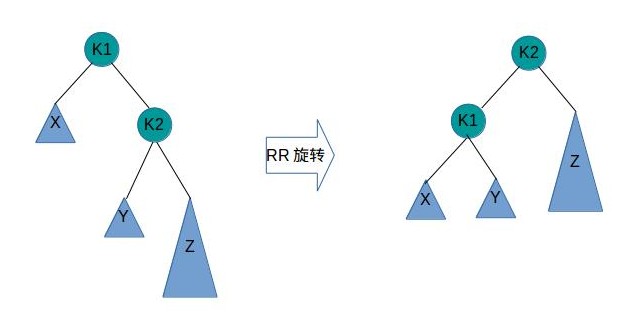
代码如下

static avl_tree_pt 
right_right_rotation(avl_tree_pt tree)
{
    avl_tree_pt right_child;

    right_child = tree->right;
    tree->right = right_child->left;
    right_child->left = tree;
    tree->height = MAX(HEIGHT(tree->left), HEIGHT(tree->right)) + 1;
    right_child->height = MAX(HEIGHT(right_child->left), HEIGHT(right_child->right)) + 1;

    return right_child;
}

LR失去平衡的情况，需要两次旋转才能让AVL树恢复平衡。如下图所示

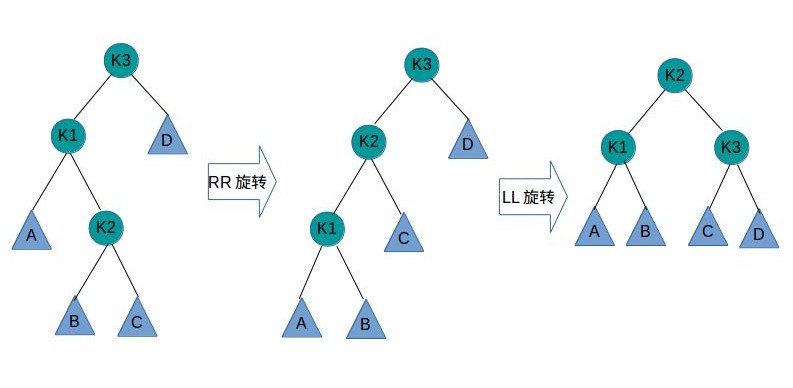
第一次旋转是围绕k1进行的RR旋转，第二次是围绕k3进行的LL旋转

代码如下

static avl_tree_pt 
left_right_rotation(avl_tree_pt tree)
{
    tree->left = right_right_rotation(tree->left);
    return left_left_rotation(tree);
}

RL失去平衡的情况，一样需要两次旋转才能让AVL树恢复平衡。如下图所示

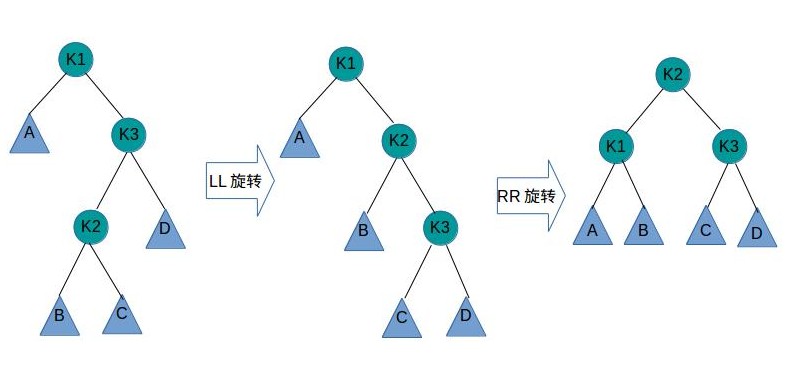
第一次旋转是围绕k3进行的LL旋转，第二次是围绕k1进行的RR旋转

代码如下

static avl_tree_pt 
right_left_rotation(avl_tree_pt tree)
{
    tree->right = left_left_rotation(tree->right);
    return right_right_rotation(tree);
}

AVL树的插入

avl_tree_pt 
avl_tree_insert(avl_tree_pt tree, Item element)
{
    if (tree == NULL) {
        tree = avl_tree_new(element, NULL, NULL);
        if (tree == NULL) {
            printf("Error: create tree node failed.\n");
        }
        return tree;
    }
    else if (item_cmp(element, tree->data)) {
        tree->left = avl_tree_insert(tree->left, element);
        if (HEIGHT(tree->left) - HEIGHT(tree->right) >= 2) {
            if (item_cmp(tree->left->data, element)) {
                tree = left_right_rotation(tree);
            }
            else {
                tree = left_left_rotation(tree);
            }
        }
    }
    else if (item_cmp(tree->data, element)) {
        tree->right = avl_tree_insert(tree->right, element);
        if (HEIGHT(tree->right) - HEIGHT(tree->left) >= 2) {
            if (item_cmp(element, tree->right->data)) {
                tree = right_left_rotation(tree);
            }
            else {
                tree = right_right_rotation(tree);
            }
        }
    }
    else {
        printf("Failed. Don't allow insert the same value.");
    }
    tree->height = MAX(HEIGHT(tree->left), HEIGHT(tree->right)) + 1;
    return tree;
}

AVL树的删除

static avl_tree_pt 
avl_node_delete(avl_tree_pt tree, avl_tree_pt node)
{
    avl_tree_pt temp;

    if (tree == NULL) {
        return NULL;
    }
    if (item_cmp(tree->data, node->data)) {
        tree->right = avl_node_delete(tree->right, node);
        if (HEIGHT(tree->left) - HEIGHT(tree->right) >= 2) {
            if (HEIGHT(tree->left->right) > HEIGHT(tree->left->left)) {
                tree = left_right_rotation(tree);
            }
            else {
                tree = left_left_rotation(tree);
            }
        }
    }
    else if (item_cmp(node->data, tree->data)) {
        tree->left = avl_node_delete(tree->left, node);
        if (HEIGHT(tree->right) - HEIGHT(tree->left) >= 2) {
            if (HEIGHT(tree->right->left) > HEIGHT(tree->right->right)) {
                tree = right_left_rotation(tree);
            }
            else {
                tree = right_right_rotation(tree);
            }
        }
    }
    else {
        if (tree->left != NULL && tree->right != NULL) {
            if (HEIGHT(tree->left) - HEIGHT(tree->right) > 0) {
                temp = avl_tree_most_right(tree->left);
                tree->data = temp->data;
                avl_node_delete(tree->left, temp);
            }
            else {
                temp = avl_tree_most_left(tree->right);
                tree->data = temp->data;
            }
        }
        else {
            temp = tree;
            tree = tree->left == NULL ? tree->right:tree->left;
            free(temp);
        }
    }
    return tree;

}

avl_tree_pt 
avl_tree_delete(avl_tree_pt tree, Item element)
{
    avl_tree_pt node;
    if ((node = avl_tree_find(tree, element)) != NULL) {
        tree = avl_node_delete(tree, node);
    }
    return tree;
}

完整源码

/* avl_tree.h */
#ifndef AVL_TREE_H
#define AVL_TREE_H

typedef int Item;

typedef struct avl_tree_s* avl_tree_pt;

typedef struct avl_tree_s {
    Item data;
    int height;
    avl_tree_pt left;
    avl_tree_pt right;
} avl_tree_t;

avl_tree_pt avl_tree_find(avl_tree_pt tree, Item element);
avl_tree_pt avl_tree_insert(avl_tree_pt tree, Item element);
avl_tree_pt avl_tree_delete(avl_tree_pt tree, Item element);
void avl_tree_destroy(avl_tree_pt tree);
void avl_tree_print(avl_tree_pt tree);
void avl_tree_export_dot(avl_tree_pt tree, char *filename, char *label);

#endif

avl_tree.h

/* avl_tree.c */
/*
 * =====================================================================================
 *
 *       Filename:  avl_tree.c
 *
 *    Description:  平衡二叉树实现
 *
 *        Version:  1.0
 *        Created:  2016-10-08 20:35
 *       Revision:  none
 *       Compiler:  gcc
 *
 *         Author:  simon
 *
 * =====================================================================================
 */

#include <stdio.h>
#include <stdlib.h>

#include "avl_tree.h"


/* 
 * 从小到大 ((a) < (b))
 * 从大到小 ({a} > (b))
 * 
 */
#define item_cmp(a, b) ((a) < (b)) /* 从小到大 */

#define HEIGHT(t) ((t) == NULL ? 0 : (t)->height)

#define MAX(a, b) ((a) > (b) ? (a) : (b))

static avl_tree_pt 
avl_tree_new(Item element, avl_tree_pt left, avl_tree_pt right)
{
    avl_tree_pt node = (avl_tree_pt)malloc(sizeof(avl_tree_t));
    if (node == NULL) {
        return NULL;
    }

    node->data = element;
    node->left = left;
    node->right = right;
    node->height = MAX(HEIGHT(node->left), HEIGHT(node->right)) + 1;

    return node;
}

static avl_tree_pt 
left_left_rotation(avl_tree_pt tree)
{
    avl_tree_pt left_child;

    left_child = tree->left;
    tree->left = left_child->right;
    left_child->right = tree;
    tree->height = MAX(HEIGHT(tree->left), HEIGHT(tree->right)) + 1;
    left_child->height = MAX(HEIGHT(left_child->left), HEIGHT(left_child->right)) + 1;

    return left_child;
}


static avl_tree_pt 
right_right_rotation(avl_tree_pt tree)
{
    avl_tree_pt right_child;

    right_child = tree->right;
    tree->right = right_child->left;
    right_child->left = tree;
    tree->height = MAX(HEIGHT(tree->left), HEIGHT(tree->right)) + 1;
    right_child->height = MAX(HEIGHT(right_child->left), HEIGHT(right_child->right)) + 1;

    return right_child;
}

static avl_tree_pt 
left_right_rotation(avl_tree_pt tree)
{
    tree->left = right_right_rotation(tree->left);
    return left_left_rotation(tree);
}

static avl_tree_pt 
right_left_rotation(avl_tree_pt tree)
{
    tree->right = left_left_rotation(tree->right);
    return right_right_rotation(tree);
}


avl_tree_pt 
avl_tree_insert(avl_tree_pt tree, Item element)
{
    if (tree == NULL) {
        tree = avl_tree_new(element, NULL, NULL);
        if (tree == NULL) {
            printf("Error: create tree node failed.\n");
        }
        return tree;
    }
    else if (item_cmp(element, tree->data)) {
        tree->left = avl_tree_insert(tree->left, element);
        if (HEIGHT(tree->left) - HEIGHT(tree->right) >= 2) {
            if (item_cmp(tree->left->data, element)) {
                tree = left_right_rotation(tree);
            }
            else {
                tree = left_left_rotation(tree);
            }
        }
    }
    else if (item_cmp(tree->data, element)) {
        tree->right = avl_tree_insert(tree->right, element);
        if (HEIGHT(tree->right) - HEIGHT(tree->left) >= 2) {
            if (item_cmp(element, tree->right->data)) {
                tree = right_left_rotation(tree);
            }
            else {
                tree = right_right_rotation(tree);
            }
        }
    }
    else {
        printf("Failed. Don't allow insert the same value.");
    }
    tree->height = MAX(HEIGHT(tree->left), HEIGHT(tree->right)) + 1;
    return tree;
}

avl_tree_pt 
avl_tree_find(avl_tree_pt tree, Item element)
{
    if (tree == NULL) {
        return NULL;
    }
    if (item_cmp(tree->data, element)) {
        avl_tree_find(tree->right, element);
    }
    else if (item_cmp(element, tree->data)) {
        avl_tree_find(tree->left, element);
    }
}

static avl_tree_pt 
avl_tree_most_left(avl_tree_pt tree)
{
    if (tree == NULL) {
        return NULL;
    }

    while (tree->left != NULL) {
        tree = tree->left;
    }
    return tree;
}

static avl_tree_pt 
avl_tree_most_right(avl_tree_pt tree)
{
    if (tree == NULL) {
        return NULL;
    }

    while (tree->right != NULL) {
        tree = tree->right;
    }
    return tree;
}

static avl_tree_pt 
avl_node_delete(avl_tree_pt tree, avl_tree_pt node)
{
    avl_tree_pt temp;

    if (tree == NULL) {
        return NULL;
    }
    if (item_cmp(tree->data, node->data)) {
        tree->right = avl_node_delete(tree->right, node);
        if (HEIGHT(tree->left) - HEIGHT(tree->right) >= 2) {
            if (HEIGHT(tree->left->right) > HEIGHT(tree->left->left)) {
                tree = left_right_rotation(tree);
            }
            else {
                tree = left_left_rotation(tree);
            }
        }
    }
    else if (item_cmp(node->data, tree->data)) {
        tree->left = avl_node_delete(tree->left, node);
        if (HEIGHT(tree->right) - HEIGHT(tree->left) >= 2) {
            if (HEIGHT(tree->right->left) > HEIGHT(tree->right->right)) {
                tree = right_left_rotation(tree);
            }
            else {
                tree = right_right_rotation(tree);
            }
        }
    }
    else {
        if (tree->left != NULL && tree->right != NULL) {
            if (HEIGHT(tree->left) - HEIGHT(tree->right) > 0) {
                temp = avl_tree_most_right(tree->left);
                tree->data = temp->data;
                avl_node_delete(tree->left, temp);
            }
            else {
                temp = avl_tree_most_left(tree->right);
                tree->data = temp->data;
            }
        }
        else {
            temp = tree;
            tree = tree->left == NULL ? tree->right:tree->left;
            free(temp);
        }
    }
    return tree;

}

avl_tree_pt 
avl_tree_delete(avl_tree_pt tree, Item element)
{
    avl_tree_pt node;
    if ((node = avl_tree_find(tree, element)) != NULL) {
        tree = avl_node_delete(tree, node);
    }
    return tree;
}

void 
avl_tree_destroy(avl_tree_pt tree)
{
    if (tree == NULL) {
        return;
    }
    avl_tree_destroy(tree->left);
    avl_tree_destroy(tree->right);
    free(tree);
}


static void 
avl_tree_printnode(avl_tree_pt node, int h)
{
    int i;
    for (i=0; i < h; i++) {
        printf("    ");
    }
    if (node == NULL) {
        printf("*\n");
    }
    else {
        printf("%d\n", node->data);
    }
}

static void 
avl_tree_show(avl_tree_pt tree, int h)
{
    if (tree == NULL) {
        avl_tree_printnode(tree, h);
        return;
    }
    avl_tree_show(tree->left, h+1);
    avl_tree_printnode(tree, h);
    avl_tree_show(tree->right, h+1);
}

void 
avl_tree_print(avl_tree_pt tree)
{
    avl_tree_show(tree, 0);
}


/* 打印节点计数变量 */
static int node_num = 0;

static void 
export_dot(FILE *fp, avl_tree_pt tree, char *last_label)
{
    /* 打印节点 */
    char node_name[10] = {0};
    sprintf(node_name, "n%d", node_num);
    if (tree == NULL) {
        fprintf(fp, "%s[style=invis];\n", node_name);
    }
    else {
        fprintf(fp, "%s[label=%d, xlabel=%d];\n", node_name, tree->data, tree->height);
    }
    node_num++;

    /* 打印边 */
    if (last_label != NULL) {
        if (tree == NULL) {
            fprintf(fp, "%s->%s[style=invis];\n", last_label, node_name);
        }
        else {
            fprintf(fp, "%s->%s;\n", last_label, node_name);
        }
    }

    if (tree == NULL) {
        return;
    }

    /* 打印子节点 */
    if (tree->left == NULL && tree->right == NULL) {
        return;
    }
    export_dot(fp, tree->left, node_name);
    export_dot(fp, NULL, node_name);
    export_dot(fp, tree->right, node_name);
}

void 
avl_tree_export_dot(avl_tree_pt tree, char *filename, char *label)
{
    FILE *fp;
    fp = fopen(filename, "w");
    fprintf(fp, "digraph g{\nnode[shape=circle];\nlabel=\"%s\";\nlabeljust=l;\nlabelloc=t;\n", label);
    export_dot(fp, tree, NULL);
    fprintf(fp, "}\n");
    fclose(fp);
}

avl_tree.c

/* avl_tree_test.c */
#include <stdlib.h>
#include <stdio.h>

#include "avl_tree.h"

#define LENGTH(a) ( (sizeof(a)) / (sizeof(a[0])) )

int
main(int argc, char *argv[])
{
    int a[] = {3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9};
    int i, len=LENGTH(a);
    avl_tree_pt tree=NULL;

    printf("== AVL树中依次添加: ");
    for(i=0; i<len; i++)
    {
        printf("%d ", a[i]);
        tree = avl_tree_insert(tree, a[i]);
    }
    avl_tree_print(tree);

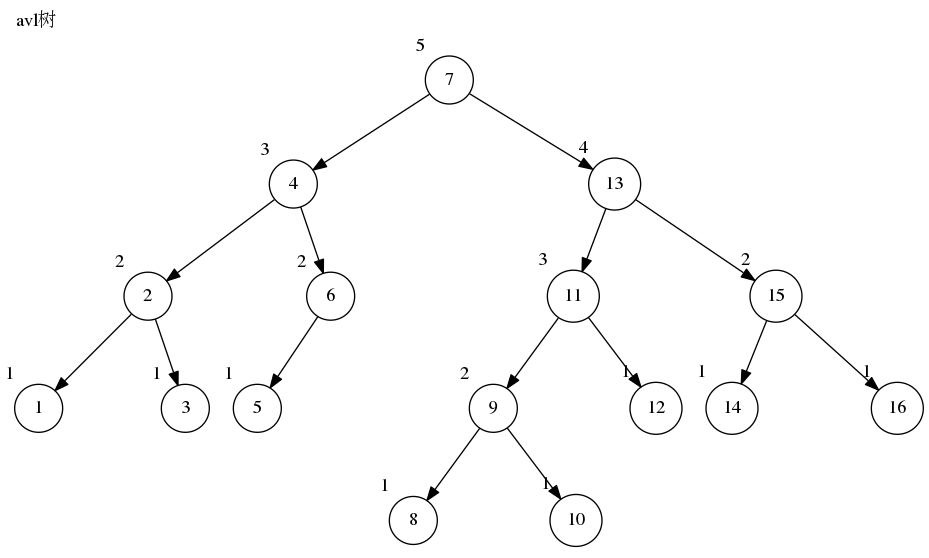
    avl_tree_export_dot(tree, "avl.dot", "avl树");

    avl_tree_destroy(tree);
    return 0;
}

avl_tree_test.c

测试程序的运行结果

== AVL树中依次添加: 3 2 1 4 5 6 7 16 15 14 13 12 11 10 8 9                 *
            1
                *
        2
                *
            3
                *
    4
                *
            5
                *
        6
            *
7
                    *
                8
                    *
            9
                    *
                10
                    *
        11
                *
            12
                *
    13
                *
            14
                *
        15
                *
            16
                *

最后生成dot标记文件，然后使用工具可以生成下图

转载文章请注明出处： http://mingnote.com

AVL树的C语言实现

失去平衡的AVL树

AVL树的旋转

AVL树的插入

AVL树的删除

完整源码

测试程序的运行结果

Date 2016-10-10(星期一) 20:55 By Ming In 算法 Tags 算法,